A Virtual Rubik's Cube

function M(x, ar =[]) {
    return function go(func) {
      if (func === dF3x) return x;
      else if (func === dF3ar) return ar;
      x = func(x);
      ar.push(func.key);
      return go;
    };
  }

The default empty array "ar" was added to the basic m-M(x) closure to work with the function reverse(). Modifying "M" wasn't necessary, but the elegant simplicity of reversing moves with the modified "M" was irresistable.

function reverse () { 
    m = m(ob[m(dF3ar).pop()]); // Pops a function name and runs its reverse.   
    m(dF3ar).pop(); // Discard the inverse functions's name, that m just 
                    // pushed onto ar (inside of the m-M(x) closure). 
  }

The version of the m-M(x) closure used on this page encapsulates an array of six nine-member arrays of the strings "blue", "green", "red", "orange", "yellow", and "white." Users have at their disposal 12 basic functions (top row below) and their inverses (bottom row).

User key presses and button clicks cause the 54 strings in the m-M(x) closure to rearrange. The virtual cube image on the right consists of 27 buttons with statements " style = 'background-color = m(dF3x)[ j ][ k ]' " for positive whole numbers j less than 6 and k less than 9. If the string at some position x[ j ][ k ] is replaced by a different string after a key press or button click, that string determines the color of the button containing the statement " style = 'background-color = m(dF3x)[ j ][ k ]' ."

Four Key-Presses / Four Button-clicks Demonstration

The 27 buttons of the virtual Rubik's cube never move.

The positions of the 54 elements of "x" in the closure change in response to user input, but the positions of the 27 buttons of the virtual Rubik's cube are permanently fixed. The 9 buttons of the outward facing side of the cube image have background colors m(dF3x)[ 3 ][ 0 ], m(dF3x)[ 3 ][ 1 ], ...m(dF3x)[ 3 ][ 8 ] starting in the upper-left button and ending in the lower-right button. As x[3] changes in the closure, so the front-facing side of the virtual Rubik's changes.

Pressing "U", "D", "R", "L", "F", or "B" keys, or clicking their corresponding buttons (above), rearranges some of the background colors of the 9 buttons that constitute each face of the virtual cube, simulating the result of turning the top, bottom, right, left, front, and back faces, respectively, of a Rubik's cube 90%. "M", "E", and "S" turn the middle sections 90 degrees. X", "Y", and "Z" turn the whole cube clockwise 90 degrees around the traditional x, y, and z axes. The single quote marks signify inverses, which can be run on the keyboard by simultaneously holding down the Shift key.

<button style="background-color: {m(dF3x)[3][3]}" 
    on:click={() => {m = m(Cyr)}} />

The elements of the array of six arrays held in the m-M(x) closure are embedded (by means of expressions "m(dF3ar)[j][k]") in the 27 buttons of the visible sides of the virtual Rubik's cube. If a user presses a key or clicks a button that calls m(func) -- thereby running x => func(x) in the m-M(x) closure -- each of the 27 copies of m in the method m (dF3ar) in the simulated Rubik's cube in the DOM immediately updates by returning the func(x). And if, for example, the string to which x[3][3] points in the closure changes from from 'green' to 'red', the value of m(dF3ar)[3][3] in the DOM will likewise change, and the color of the left square in the second row of the forward facing of the virtual Rubik's cube will be observed to change from red to green.

The nine strings of the array x[3] correspond exactly to the nine buttons constituting the front of virtual Rubik's cube. These are all orange on the starting and solved cube.

function reverse () { 
    m = m(ob[m(dF3ar).pop()]); // Pops a function name and runs its reverse.   
    m(dF3ar).pop(); // Discard the inverse functions's name, that m just 
                    // pushed onto ar (inside of the m-M(x) closure). 
  }

The object ob contains 24 key:value pairs of the names and inverses of the functions that exchange and rearrange the elements of the six nine-member arrays of strings that constitute x in the m-M() closure.

const ob = {'R': Rz, 'L': Lz, 'U': Uz, 'D': Dz, 'F': Fz, 'B': Bz, 'Cx': Cxr,
   'Cy': Cyr, 'Cz': Czr, 'Xro': Xror, 'Yro': Yror, 'Zro': Zror, 'Rz': R,
   'Lz': L, 'Uz': U, 'Dz': D, 'Fz': F, 'Bz': B, 'Cxr': Cx, 'Cyr': Cy, 'Czr': Cz,
   'Xror': Xro, 'Yror': Yro, 'Zror': Zro};

Callbacks Rearrange x in the m-M(x) Closure

Clicking the "Start" button (or pressing "V") refreshes the m-M(x) closure by declaring "m = M(x)" where

 x = [ ['blue','blue','blue','blue','blue','blue','blue','blue','blue'],  // Right side
['green','green','green','green','green','green','green','green','green'],
['red','red','red','red','red','red','red','red','red'],
['orange','orange','orange','orange','orange','orange','orange','orange','orange'],   // Front
['yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow'],  // Top
['white','white','white','white','white','white','white','white', 'white'] ] 

x[0], x[3], and x[4] correspond to the right side, front, and top faces of the cube, respectively. Pressing the "F" key calls m(F), causing the value of x (whatever it happens to be at the time) to update to F(x) in the m-M(x) closure. Corresponding to the rearrangement of x (see above), the front face of the cube will seem to have rotated clockwise 90 degrees. Here's the definition of "F."

The Browser Image

Here's the HTML code for the Rubik's cube image on the right:

<div class="face front">
  <div class="grid">
    <button style="background-color: {m(dF3x)[3][0]}" on:click={() => {m = m(Fz)}}/>
    <button style="background-color: {m(dF3x)[3][1]}" on:click={() => {m = m(Cx)}}/>
     <button style="background-color: {m(dF3x)[3][2]}" on:click={() => {m = m(F)}}/>
     <button style="background-color: {m(dF3x)[3][3]}" on:click={() => {m = m(Cyr)}}/>
     <button style="background-color: {m(dF3x)[3][4]}" on:click={() => {m = m(Zro)}}/>
     <button style="background-color: {m(dF3x)[3][5]}" on:click={() => {m = m(Cy)}}/>
     <button style="background-color: {m(dF3x)[3][6]}" on:click={() => {m = m(Fz)}}/>
     <button style="background-color: {m(dF3x)[3][7]}" on:click={() => {m = m(Cxr)}}/>
     <button style="background-color: {m(dF3x)[3][8]}" on:click={() => {m = m(F)}}/>
  </div>
</div>

<div class="face right">
  <div class="grid">
    <button style="background-color: {m(dF3x)[0][0]}" on:click={() => {m = m(Rz)}}/>
    <button style="background-color: {m(dF3x)[0][1]}" on:click={() => {m = m(Cz)}}/>
    <button style="background-color: {m(dF3x)[0][2]}" on:click={() => {m = m(R)}}/>
    <button style="background-color: {m(dF3x)[0][3]}" on:click={() => {m = m(Cyr)}}/>
    <button style="background-color: {m(dF3x)[0][4]}" on:click={() => {m = m(Xro)}}/>
    <button style="background-color: {m(dF3x)[0][5]}" on:click={() => {m = m(Cy)}}/>
    <button style="background-color: {m(dF3x)[0][6]}" on:click={() => {m = m(Rz)}}/>
    <button style="background-color: {m(dF3x)[0][7]}" on:click={() => {m = m(Czr)}}/>
    <button style="background-color: {m(dF3x)[0][8]}" on:click={() => {m = m(R)}}/>
  </div>
</div>

<div class="face top">
  <div class="grid">
    <button style="background-color: {m(dF3x)[4][0]}" on:click={() => {m = m(Uz)}}/>
    <button style="background-color: {m(dF3x)[4][1]}" on:click={() => {m = m(Cx)}}/>
    <button style="background-color: {m(dF3x)[4][2]}" on:click={() => {m = m(U)}}/>
    <button style="background-color: {m(dF3x)[4][3]}" on:click={() => {m = m(Cz)}}/>
    <button style="background-color: {m(dF3x)[4][4]}" on:click={() => {m = m(Yro)}}/>
    <button style="background-color: {m(dF3x)[4][5]}" on:click={() => {m = m(Czr)}}/>
    <button style="background-color: {m(dF3x)[4][6]}" on:click={() => {m = m(Uz)}}/>
    <button style="background-color: {m(dF3x)[4][7]}" on:click={() => {m = m(Cxr)}}/>
    <button style="background-color: {m(dF3x)[4][8]}" on:click={() => {m = m(U)}}/>
  </div>        
</div>

Changing x in the m-M(x) JavaScript closure changes m(dF3x) embedded in the HTML code for the cube because they both point to the same place in memory. x === m(dF3x) returns "true." on in memory. Changing the value of x changes the value of m(dF3x) and vice versa.

The 27 buttons constituting the visible half of the simulated Rubik's cube never move. Pressing "Y" when the cube is in the starting configuration rearranges background colors to this configuration:

Press "Y" again and see this:

x[0] went from all blue (in the starting configuration), to all red (code is below) to all green (a little further down).

  x = [ ['red','red','red','red','red','red','red','red','red'],  // Right side
  ['orange','orange','orange','orange','orange','orange','orange','orange','orange'],
  ['green','green','green','green','green','green','green','green','green'],
  ['blue','blue','blue','blue','blue','blue','blue','blue','blue'],   // Front
  ['yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow'],  // Top
  ['white','white','white','white','white','white','white','white', 'white'] ] 

And then ...

  x = [ ['green','green','green','green','green','green','green','green','green'],  // Right side
  ['blue','blue','blue','blue','blue','blue','blue','blue','blue'],
  ['orange','orange','orange','orange','orange','orange','orange','orange','orange'],
  ['red','red','red','red','red','red','red','red','red'],   // Front
  ['yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow','yellow'],  // Top
  ['white','white','white','white','white','white','white','white', 'white'] ] 

x[3]'s background colors went from orange to blue to red. The cube seems to have rotated, but all of the divs and buttons remained stationary. Rearranging strings in the m-M(x) closure by pressing "Y", thereby rearranging the background colors of some of the simulated Rubik's cube buttons, created the illusion.

async function fmoves (ar, t = 100, f=m) { // Pauses for 100 microseconds.
        f(dF3ar).length = 0;              // Empties ar
        for (let k = 0; k < ar.length ; k += 1) {
            await wait(t);
            f = m(ar[k]);
        };
    };

Continued from the previous page

Rotating the Left, Back, and Bottom Faces

METHOD ONE -- The fastest method:

The left, back, and bottom faces can be turned clockwise by pressing L, B, and D, respectively. Hold down the SHIFT key for counterclockwise rotation.

METHOD TWO -- clicking the cube

Click the top center 3 times to bring the green face forward.
      Click the right top or bottom square.
      Click the top center 3 more times, bringing the red face forward.
      Click the right top or bottom square.
      Click the top center two times to re-orient the cube.
      Click the right center to bring up the bottom face.
      Click the right top or bottom square.
      Click the right center 3 more times to re-orient the cube.

This is the expected result of pressing "LBD" or following the instructions of Method 2 (above):

The Amazing Reverse Function

Here's the function "reverse":

function reverse () { 
    m = m(ob[m(dF3ar).pop()]); // Pops a function name and runs its reverse.   
    m(dF3ar).pop(); // Discard the inverse functions's name, that m just 
                    // pushed onto ar (inside of the m-M(x) closure). 
  }

And this is the key-value lookup table:

const ob = {'R': Rz, 'L': Lz, 'U': Uz, 'D': Dz, 'F': Fz, 'B': Bz, 'Cx': Cxr,
   'Cy': Cyr, 'Cz': Czr, 'Xro': Xror, 'Yro': Yror, 'Zro': Zror, 'Rz': R,
   'Lz': L, 'Uz': U, 'Dz': D, 'Fz': F, 'Bz': B, 'Cxr': Cx, 'Cyr': Cy, 'Czr': Cz,
   'Xror': Xro, 'Yror': Yro, 'Zror': Zro};

The array of six nine-member arrays of strings held in the m-M(x) closure is transformed whenever a user presses certain keys, or clicks the mouse over buttons or various parts of the displayed cube image. These actions call m(func) for functions "func" that rearrange strings in the m-M(x) closure, making it seem as though the virtual Rubik's cube, one of its six sides, or one of its three middle sections have rotated 90 degrees. This works because the strings in the m-M(x) closure are exposed in "background-color = m(dF3x)[j][k]" statements for 0 and positive integers j less than 6 and k less than nine, in the 27 buttons that constitute the visible faces of the virtual Rubik's cube seen in the browser.

Note: The attributes "key" that were added to each function discussed above are identical to the built-in string attributes "name." Running "build" mutated the name attributes, making it necessary to add the redundant "key" attributes.

Here's a screenshot of function logged into Firefox Developer Tools (accessed by pressing F12).

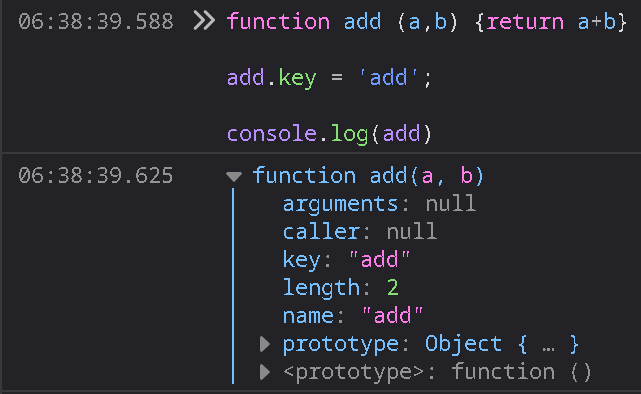
I had to add the "key" attribute. Why SvelteKit build mangles func.name but not my added func.key escapes me. I'm glad that whoever "optimized" SvelteKit this way spared developer-added attributes.

The efficiency of the "reverse" function can be observed by clicking "Scramble" or pressing the "W" a few times, and then holding down the "Q" key. You can watch the simulated cube perform 40 X the number of scrambles reverse moves in several seconds.

function reverse () { 
    m = m(ob[m(dF3ar).pop()]); // Pops a function name and runs its reverse.   
    m(dF3ar).pop(); // Discard the inverse functions's name, that m just 
                    // pushed onto ar (inside of the m-M(x) closure). 
  }

*********************************************************

After solving the first two layers, if you happen to have one of the 24 possible 'L' shapes, or one the 16 possible bar shapes on top, you can watch an automated solution go to completion. Here's how: (1) Turn the orange two layers toward you by pressing the "Y" key. (2) If you have an "L" shape on top, click the "Solve L" button below. (3) If you have a bar shape on top, click the "Solve Bar" button below.

Here are some additional feature that might interest you: (4) Click the "King" buttons (below) to see the possible "L" and bar configurations. (5) If pressing the "F12" key loads a developer-tools screen, you can watch the log of progress unfold in the console. To see the log in Firefox after clicking "King 6" and pressing "U" three times, go to the bottom of this page.

Clicking "Solve L" causes it will call U(), turning your cube's top 90 degrees, and try again. If there is still no match after trying two more 90 degree turns, it will move on to king_2. It keeps going until it finds a match and shows the solution. If it gets all the way to king_6 and the first three tries fail, it's a sure bet that the 24th attempt will succeed.

You can test this by clicking "king_6", pressing 'U' three times, the then clicking (Solve L). If pressing F12 makes a console available, you can see the log of 23 test failurs and then then, one by one, the moves that complete the solution.

Here's another demonstration: click "king.L1" and then "Solve L". "In compare1" is displayed and "F,R,U,Rz,Uz,R,U,Rz,Uz,Fz" appears incrementally while the functioins with those names operate on x in the m-M(x) closure.

Now click "king.L1" again, followed by "king.L2st" and then "Solve L." This time, "In compare4" displays, indicating king.L4st is solving the (king.L1, king.L2st) configuration. And, that's what happens.

But wait! Clicking king.L1, king.L2st, then king.L4st (quotation marks were annoying me) doesn't solve the king.L2st(king.L1) configuration.

Pressing F12 reveals that "Solve L" fails, runs "U", fails, runs "U" again, and then begins calling the king.L4st functions (Rz, Cx, U, ...) that solve the cube.

The buttons below run the standard OLL algorithms on the current cube configuration. You can ignore them. Just turn the orange side toward yourself (press the "Y" key) and click "Solve L" or "Solve Bar". Each algorithm will be tried, with 0, 1, 2, and 3 90 degree turns of the top layer until a solution is found or "FAIL" is displayed. The default milliseconds between turns is 30. You can change that here:

pause interveral now is 300 milliseconds
You can enter a different number of milliseconds here:

backforth Solve L Solve Bar

R,Rz

"L" Patterns

OLL47 OLL48 OLL49 OLL50 OLL53 OLL54

fOLL47 fOLL48 fOLL49 fOLL50 fOLL53 fOLL54

Line Patterns

LL51 LL52 LL55 LL56

fOLL51 fOLL52 fOLL55 fOLL56

R,Rz

Dot Patterns

LL1 LL2 LL3 LL4 LL17

LL18 LL19 LL20

fOLL1 fOLL2 fOLL3 fOLL4 fOLL17 fOLL18 fOLL19 fOLL20

Special Buttons

log x log ar log nn test8

This is the archive:

You

*********************************************************

Clicking L1, L2, ... or L6 displays one of the six commonly encountered last-layer L configurations. Clicking "Solve L"

LL51

Welcome to access Lunabot, the chatbot for your website. You can ask me anything, and I will try my best to answer you.

LL52 Web app is released: https://lunabot.ai/webapF,U,R,Uz,Rz,U,R,Uz,Rz,Fzp

My question: This question is about algorithms for completing the last layer of a Rubik's cube. One gets the impression that only 57 algorithms are required. Only six algorithms are presented for the "L" configuration. It's easy to configure the cube into an L shape that these algorithms don't solve. For example, take any "L" configuration x and run the algorithm for swapping opposite edges. The algorithm that solves x doesn't work. Neither do any of the other published algorithms for solving "L" configurations. What is going on? Am I missing something? Lunabot's answeer: It sounds like you may be encountering a specific case or scenario that the published algorithms for solving the "L" configuration don't cover. It's not uncommon for certain algorithms to work for a majority of cases but not all possible permutations. In this case, it's possible that the specific "L" configuration you are encountering requires a different algorithm or a combination of algorithms to solve. It's also possible that there may be alternate algorithms or methods for solving such cases that are not widely published. If you're encountering a specific case that the published algorithms don't solve, you may want to try searching for alternative algorithms or methods, or consider experimenting with different sequences of moves to see if you can find a solution. Additionally, there are many online communities and resources dedicated to Rubik's cube solving, so seeking help from other enthusiasts or experts in those forums may also provide valuable insight and alternative solutions to your specific case. Gemini My follow-up question: In the case I presented, running the algorithm for swapping opposite corners followed by the algorithm for solving x does the job. Lunabot's comment: That's great to hear! It sounds like you've found a solution to the specific "L" configuration that works for you. Experimenting with different combinations of algorithms and sequences of moves can often lead to discovering alternative solutions to specific cases that may not be covered by standard algorithms. import OLL52 from "$lib/OLL52.png";

*********************************************************

400,000 rotations (10,000 scrambles) in 0 milliseconds.

10,000 Scrambles
     Move list length: 2

function et2() {
    var start = new Date();
    let k;
    for (k = 0; k < 10000; k++) {
      shu();
    }
    elapsedTime = new Date() - start;
    return elapsedTime;
  }

GPT 3.5
How many Rubik's cube last-layer configurations cannot be solved using the 57 common algorithms?

There are 43,252,003,274,489,856,000 (approximately 43 quintillion) possible combinations for the last layer of a Rubik's cube. The 57 common algorithms are designed to solve the majority of these configurations, but there will still be a significant number of configurations that cannot be solved using these algorithms. It is difficult to accurately determine the exact number of unsolvable configurations, but it is safe to assume that a large percentage of the 43 quintillion possibilities will not be solvable using the 57 common algorithms. GPT 3.5

So OLL websites that say the probabilities of most of the configurations corresponding to the popular 57 algorithms are 1/57

I'm not sure what you mean by "OLL websites," but if you're referring to websites that provide information on the OLL (Orientation of Last Layer) algorithms for solving the Rubik's Cube, it's important to note that the probabilities of specific algorithm configurations are not likely to be exactly 1/57.

The probability of a specific algorithm configuration depends on a variety of factors, including the initial state of the Rubik's Cube, the sequence of moves used to reach that state, and the particular algorithm being applied. As such, it's unlikely that the probability would be exactly 1/57 for most configurations.

It's possible that the 1/57 figure is being used in a more general context, such as to represent the likelihood of encountering a specific OLL case in a random solve. However, it's important to approach such statistics with a critical eye and consider the specific context in which they are being presented.